The reason why undisputed isn't undisputed for bleed damage

[Oeller]

Hey everyone,

recently on the discord there again was a dicussion if Undisputed is the best weapon for bleed damage. I decided to make some short evaluation and plots to show that a not-exalted Nagasa Symitar is better most of the time while providing another open suffix for utility.

Undisputed

• 1.05 base attack rate
• Chance to bleed (implicit, 12 - 30%)
• Increased attack speed (20 - 27%)
• Up to 255% increase physical damage from buff effect

Optimal Nagasa (T15 + X)

• 1.24 base attack rate
• Increased damage over time (implicit, 26 - 56%)
• Increased physical (70 - 105%)
• Increased attack speed (21 - 26%)
• Chance to Bleed on Hit (40 - 53%)
• Suffix of choice; possibly health on hit or ignite on hit

Optimal case for Undisputed

• 51/4 hits per second → 255% increase from undisputed
• Requires an attack rate of 0.0784313725 in a single target fight
• Default attack rate: 0.68182
• Undisputed default attack rate (5% more attack speed, 27% increased attack speed): 0.511301087
• Solving 0.68182 / 1.05 / (1. + 0.27 + x) == 0.0784313725 yields x = 7.00924286 → 701% increased attack speed required to reach breakpoint
• Best case will rarely be achieved in a single target fight; even though most attacks are a little faster than default attack; doubled default attack rate (Warpath) still requires 350% increased attack speed

Dual wielding: Undisputed + Nagasa → Two Nagasa

• 8.2% more hits (8.2% more damage) → 55/4 hits per second
• 255% - (56% + 105%) = 94% → -94% increased damage for bleeds
• +23% bleed on hit chance
• Increase attack speed difference at best 1% (not accounted for)

Single weapon: Undisputed → Nagasa

• 18% more hits (18% more damage) → 60/4 hits per second
• 255% - (56% + 105%) = 94% → -94% increased damage for bleeds
• +23% bleed on hit chance
• Increase attack speed difference at best 1% (not accounted for)

Numerics

• Dual Wielding assumes Nagasa in Offhand (1.24 default attack rate)
• Attack rate with Undisputed normalized to 1
• Bleed damage normalized to 1
• More multipliers and similar stats like bleed effect/duration can be neglected as they are multiplicative
• Simplified damage formula:
  damage = (1. + increase_damage / 100) * (attack_rate) * (bleed_on_hit_chance / 100)
  • Undisputed: attack_rate = 1.
  • Dual Wield Nagasa: attack_rate = 1.082
  • Single Nagasa: attack_rate = 1.18
• Relative damage increase when replacing Undisputed with a T15 Nagasa (-94% increase, +23% chance to bleed, more attack speed):
  • Dual Wield:
    z = ((1. + x / 100 - 0.94) * 1.082 * (y / 100 + 0.23)) / ((1. + x / 100) * y / 100)
  • Sword and Board:
    z = ((1. + x / 100 - 0.94) * 1.18 * (y / 100 + 0.23)) / ((1. + x / 100) * y / 100)
  • x = increases, y = bleed chance

Visualized

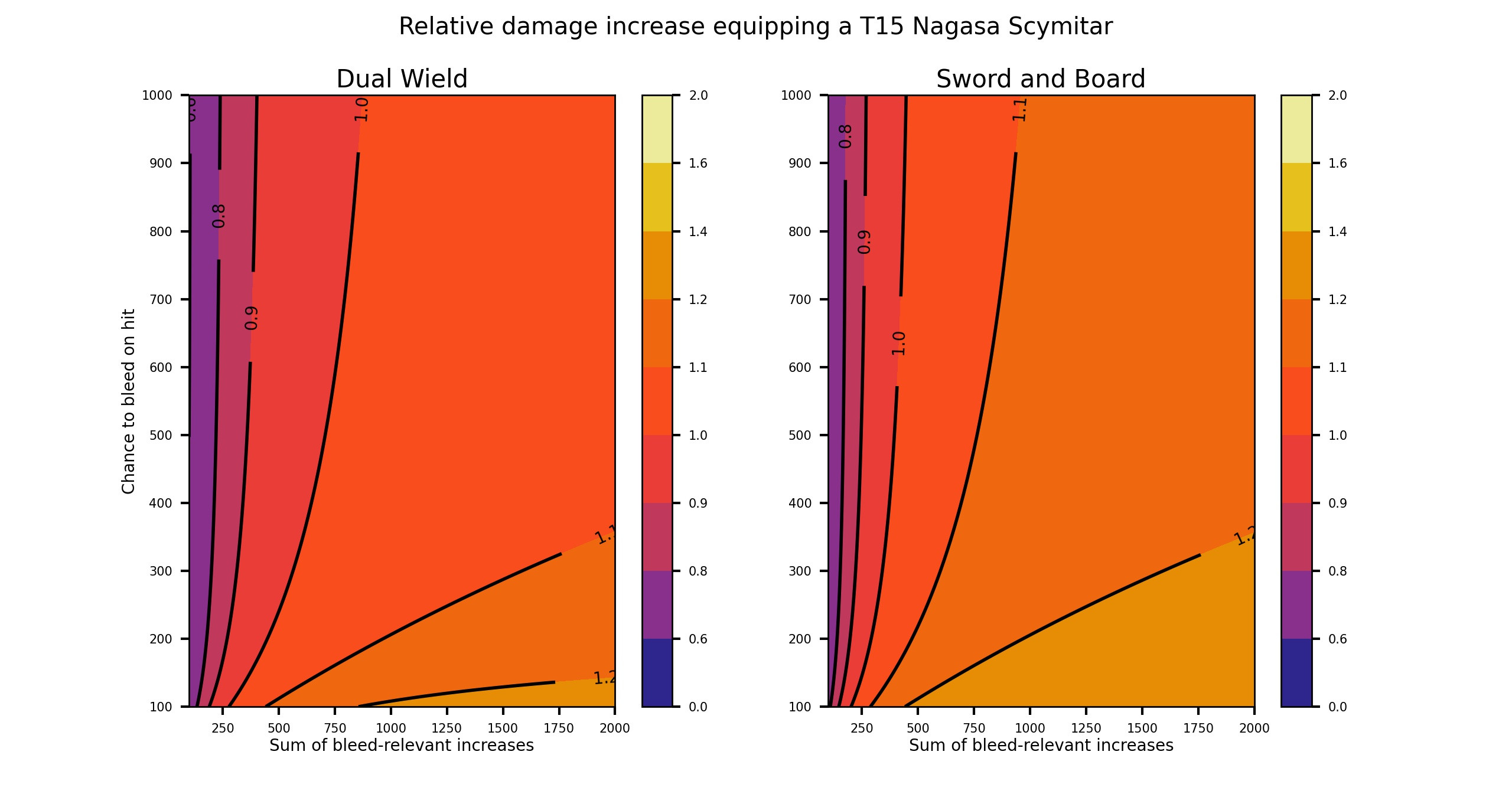
The following image show your relative damage increase when switching from an Undisputed to a T15 + X Nagasa like described above.

The values you have to look on the x and y axes are the stats you have while you have the Undisputed equipped. For x you must sum up all increases of the type generic, physical, damage over time and physical damage over time provided by gear and skills which apply the bleed (mostly attribute increases as the others generally provide more multipliers). Do not trust the character sheet since some increases are added to multiple rubrics.

[Shrukn]

I used Taste of Blood axe on my bleed Paladin, stacking double affix idols ‘Physical damage over time’ and ‘Increased duration of Bleeds’ the axe doubles bleed stack speed and gives bleed duration, always performed better than Undisputed for me because it does more burst bleed but falls off really fast

[Oeller]

Taste of Blood may feel better at some point but dps-wise it will be generally worse as the ace itself does not provide a lot of stats. Especially if you already stack duration the duration increase from the axe itself will only provide a damage increase of around 5-10% more damage. The additional bleed on melee hit is probably already beaten by the increased attackspeed on Unidsputed or a Nagasas and the Nagasa itself can have more bleed chance on T6/7 items making it far superior.

Not saying that it cannot feel better. Especially for short fights but the duration<->damage tradeoff changes nothing in your overall dps in infinite fights. Neither does it change your overall damage. It only speeds up your damage in short fights and thus can result in a dps increase in the beginning.
Note: A dps increase in the beginning does not mean you deal more damage. The damage is just distributed differently over time.

What effectively only changes by using the weapon is the way you deal damage after leaving the enemy. If you continously fight a mob with a Taste of Blood or an Axe without the duration<->damage stat you will see the same numbers as long as you hit the mob (after some ramp up time). As the trade-off for higher ticks are less bleed stacks on the enemy.

If you leave the enemy you will see your bleed dps front loaded with Taste of Blood while other weapons have a more smoothend out curve. Taste of blood results in a exponential reduction of the size of your bleed ticks while others have a linear reduction.

In the end this means if you leave use a Taste of Blood an leave the enemy and it dies of the bleed ticks it would also have die of the bleed ticks with another weapon but maybe after 6s instead of 2.